[알고리즘] 5. 동적 계획법

in 알고리즘




1. 동적 계획법 (Dynamic programming)

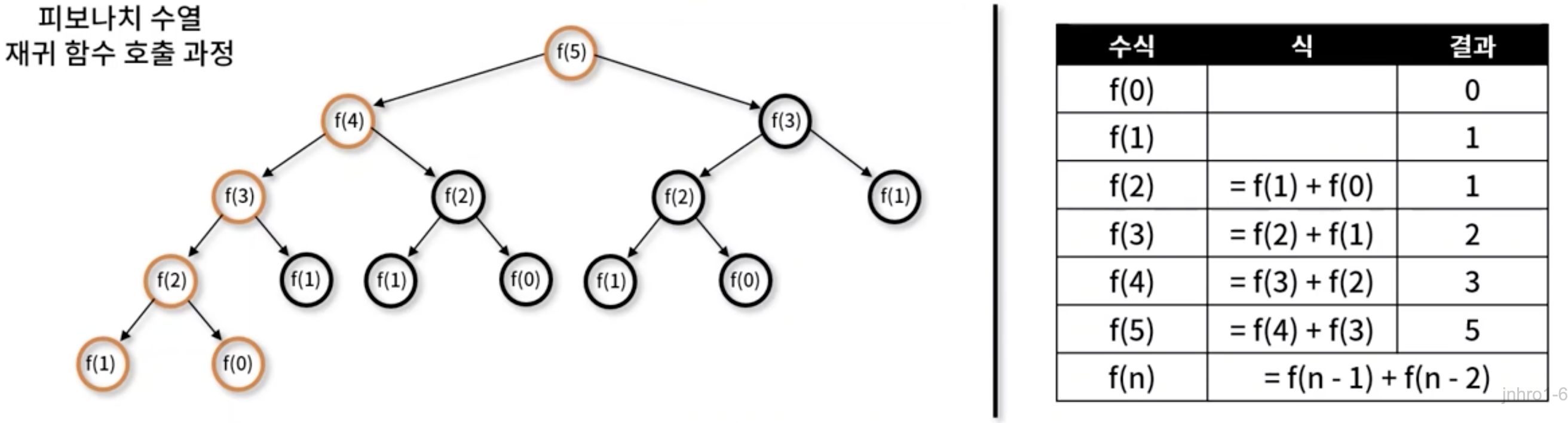
동적계획법

  • Memorization으로 중복 연산을 방지하며, 작은 부분 문제로 큰 문제를 해결하며 해를 도출하는 알고리즘 설계 기법
  • 부문 문제는 중복되며, 상위 문제 해결 시 재사용
  • Memoriaion 기법을 사용 (동일한 계산을 반복할 때, 이전에 계산한 값을 메모리에 저장하여 중복 연산 방지)
  • 점화식을 기본으로 코드를 작성한다.



동적 계획법 구현 방석

  • Top-down : 재귀를 통해 큰 문제를 작은 문제로 나눠 해결하며 해를 찾는 방법
function fibo_td(n, d = []){
    if (n<2) return n
    if (d[n]) return d[n]

    d[n] = fibo_td(n-1) + fibo_td(n-2)
    return d[n]
}

console.log(fibo_td(5)) //5
console.log(fibo_td(6)) //8
console.log(fibo_td(7)) //13


  • Bottom-up : 반복문을 통해 작은 문제부터 차례대로 해를 찾는 방법
function fibo_bu(n, d = []){
    d[0] = 0
    d[1] = 1

    for (let i =2; i<=n; i++){
        d[i] = d[i-1] + d[i-2]
    }
    return d[n]
}

console.log(fibo_bu(5)) //5
console.log(fibo_bu(6)) //8
console.log(fibo_bu(7)) //13



2. 문제 - 거스름돈🤔

programmers 

function solution(n, money) {
  let dp = new Array(n + 1).fill(0);
  dp[0] = 1;

  for (let coin of money) {
    for (let price = coin; price <= n; price++) {
      dp[price] += dp[price - coin];
    }
  }
  return dp[n] % 1000000007;
}



3. 정수 삼각형🤔

programmers 

function solution(triangle) {
  let answer = 0;
  let height = triangle.length;
  let d = Array(501)
    .fill(0)
    .map(() => Array(501).fill(0));
  answer = d[0][0] = triangle[0][0];
  for (let i = 1; i < height; i++) {
    for (let j = 0; j <= i; j++) {
      if (j == 0) {
        d[i][j] = d[i - 1][j] + triangle[i][j];
        console.log(d[i][j]);
      } else if (j == i) {
        d[i][j] = d[i - 1][j - 1] + triangle[i][j];
        console.log(d[i][j]);
      } else {
        d[i][j] = Math.max(d[i - 1][j - 1], d[i - 1][j]) + triangle[i][j];
      }
      answer = Math.max(answer, d[i][j]);
    }
  }

  return answer;
}

const tc = [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]];
console.log(solution(tc)); //30