[알고리즘] 2. 이진 검색
in 알고리즘
1. 이진 검색 (Binary Search)
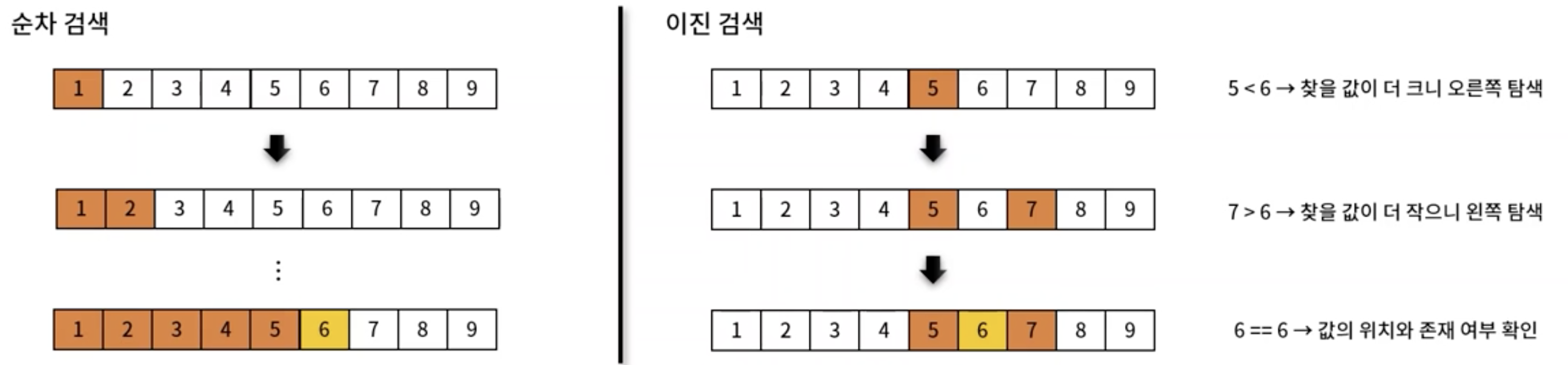
- 자료 구조 기반으로
정렬되어 있는데이터 안에서 특정 값을 찾는 기법 - 평균 시간 복잡도 : O(logN)
구현 방법 및 메소드
- 반복문을 이용한 검색 : binarySearch_loop()
- 재귀를 이용한 검색 : binarySearch_recursive()
2. 반복문 기반의 이진 검색
// binarySearch_loop() : 반복문 기반의 이진 검색
function binarySearch_loop(arr, n) {
let lowIndex = 0;
let midIndex = 0;
let highIndex = arr.length - 1;
while (lowIndex <= highIndex) {
midIndex = Math.floor((lowIndex + highIndex) / 2);
if (arr[midIndex] > n) {
highIndex = midIndex - 1;
} else if (arr[midIndex] < n) {
lowIndex = midIndex + 1;
} else {
return midIndex;
}
}
return -1;
}
// test code
let array = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
console.log(binarySearch_loop(array, 0)); //0
console.log(binarySearch_loop(array, 3)); //3
console.log(binarySearch_loop(array, 7)); //7
console.log(binarySearch_loop(array, 10)); //-1
3. 재귀 함수 기반의 이진 검색
// binarySearch_recursive() : 재귀 함수 기반의 이진 검색
function binarySearch_recursive(
arr,
n,
lowIndex = 0,
highIndex = arr.length - 1
) {
if (highIndex < lowIndex) return -1;
let midIndex = Math.floor((lowIndex + highIndex) / 2);
if (arr[midIndex] > n) {
return binarySearch_recursive(arr, n, lowIndex, midIndex - 1);
} else if (arr[midIndex] < n) {
return binarySearch_recursive(arr, n, midIndex + 1, highIndex);
} else {
return midIndex;
}
}
// test code
let array = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
console.log(binarySearch_recursive(array, 0)); //0
console.log(binarySearch_recursive(array, 3)); //3
console.log(binarySearch_recursive(array, 7)); //7
console.log(binarySearch_recursive(array, 10)); //-1
4. 문제 - 입국심사
function solution(citations) {
var answer = 0;
citations.sort((x, y) => y - x);
for (let i = 0; i < citations.length; i++) {
if (citations[i] >= i + 1) answer = i + 1;
}
return answer;
}
