// bfs() : DFS 탐색
Graph.prototype.bfs = function (startVertex) {
  this._bfsLoopVisit(startVertex);
};

// _bfsLoopVisit() : 큐를 이용한 BFS 탐색
Graph.prototype._bfsLoopVisit = function (vertex) {
  let queue = new Queue();
  queue.enqueue(vertex);

  while (!queue.isEmpty()) {
    let vertex = queue.deuqeue();
    if (this.visited[vertex]) {
      continue;
    }
    this.visited[vertex] = true;
    console.log(`visit "${vertex}"`);

    let neighbors = this.edge[vertex];

    for (let i = 0; i < neighbors.length; i++) {
      queue.enqueue(neighbors[i]);
    }
  }
};

let graph = new Graph();
let vertices = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];

for (let i = 0; i < vertices.length; i++) {
  graph.addVertex(vertices[i]);
}

graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("E", "I");

graph.print();
console.log("");

graph.bfs("A");
// visit "A"
// visit "B"
// visit "C"
// visit "D"
// visit "E"
// visit "F"
// visit "G"
// visit "H"
// visit "I"

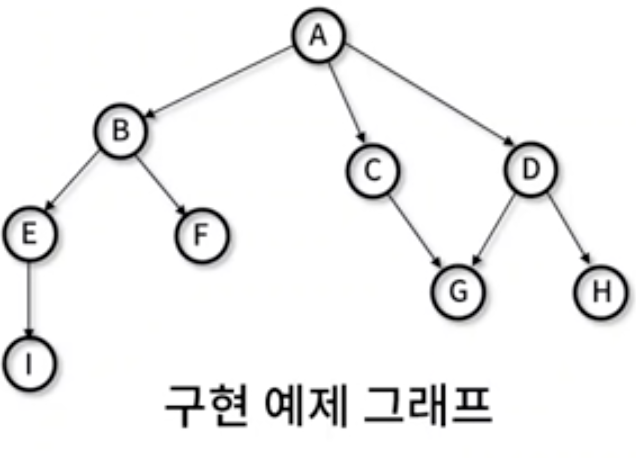
// _bfsShortesPath() : 다른 정점 간 최단 경로 비용 산출
Graph.prototype._bfsShortesPath = function (vertex) {
  let queue = new Queue();
  queue.enqueue(vertex);

  let distance = {};
  let pre_visit = {};
  for (let vertex in this.edge) {
    distance[vertex] = 0;
    pre_visit[vertex] = null;
  }

  while (!queue.isEmpty()) {
    let vertex = queue.deuqeue();
    this.visited[vertex] = true;
    console.log(`visit "${vertex}"`);

    let neighbors = this.edge[vertex];

    for (let i = 0; i < neighbors.length; i++) {
      if (!this.visited[neighbors[i]]) {
        distance[neighbors[i]] = distance[vertex] + 1;
        pre_visit[neighbors[i]] = vertex;
        queue.enqueue(neighbors[i]);
      }
    }
  }
  return { distance, pre_visit };
};

// _from_to_path() : from 정점에서 to 정점으로 최단 경로 출력
Graph.prototype._from_to_path = function (pre_visit, from, to) {
  let stack = new Stack();

  for (let v = to; v !== from; v = pre_visit[v]) {
    stack.push(v);
  }
  stack.push(from);

  while (!stack.isEmpty()) {
    let v = stack.pop();
    process.stdout.write(`${v} -> `);
  }
  console.log("end");
};

// shortestPath() : 다른 정점 간 최단 경로 탐색
Graph.prototype.shortestPath = function (startVertex) {
  let result = this._bfsShortesPath(startVertex);

  console.log(result.distance);
  console.log(result.pre_visit);

  for (let vertex in this.edge) {
    if (vertex === startVertex) continue;

    this._from_to_path(result.pre_visit, startVertex, vertex);
  }
};


let q = new Queue();
console.log("q", q.isEmpty());

let graph = new Graph();
let vertices = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];

for (let i = 0; i < vertices.length; i++) {
  graph.addVertex(vertices[i]);
}

graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("E", "I");

// graph.print();
// console.log("");

console.log(graph._bfsShortesPath("A"))
// {
//   distance: { A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2, I: 3 },
//   pre_visit: {
//     A: null,
//     B: 'A',
//     C: 'A',
//     D: 'A',
//     E: 'B',
//     F: 'B',
//     G: 'D',
//     H: 'D',
//     I: 'E'
//   }
// }

graph.shortestPath("A");
// visit "A"
// visit "B"
// visit "C"
// visit "D"
// visit "E"
// visit "F"
// visit "G"
// visit "G"
// visit "H"
// visit "I"
// { A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2, I: 3 }
// {
//   A: null,
//   B: 'A',
//   C: 'A',
//   D: 'A',
//   E: 'B',
//   F: 'B',
//   G: 'D',
//   H: 'D',
//   I: 'E'
// }
// A -> B -> end
// A -> C -> end
// A -> D -> end
// A -> B -> E -> end
// A -> B -> F -> end
// A -> D -> G -> end
// A -> D -> H -> end
// A -> B -> E -> I -> end