[비선형] 1. 트리

in 자료구조 on 비선형




1. 트리 (Tree)

트리

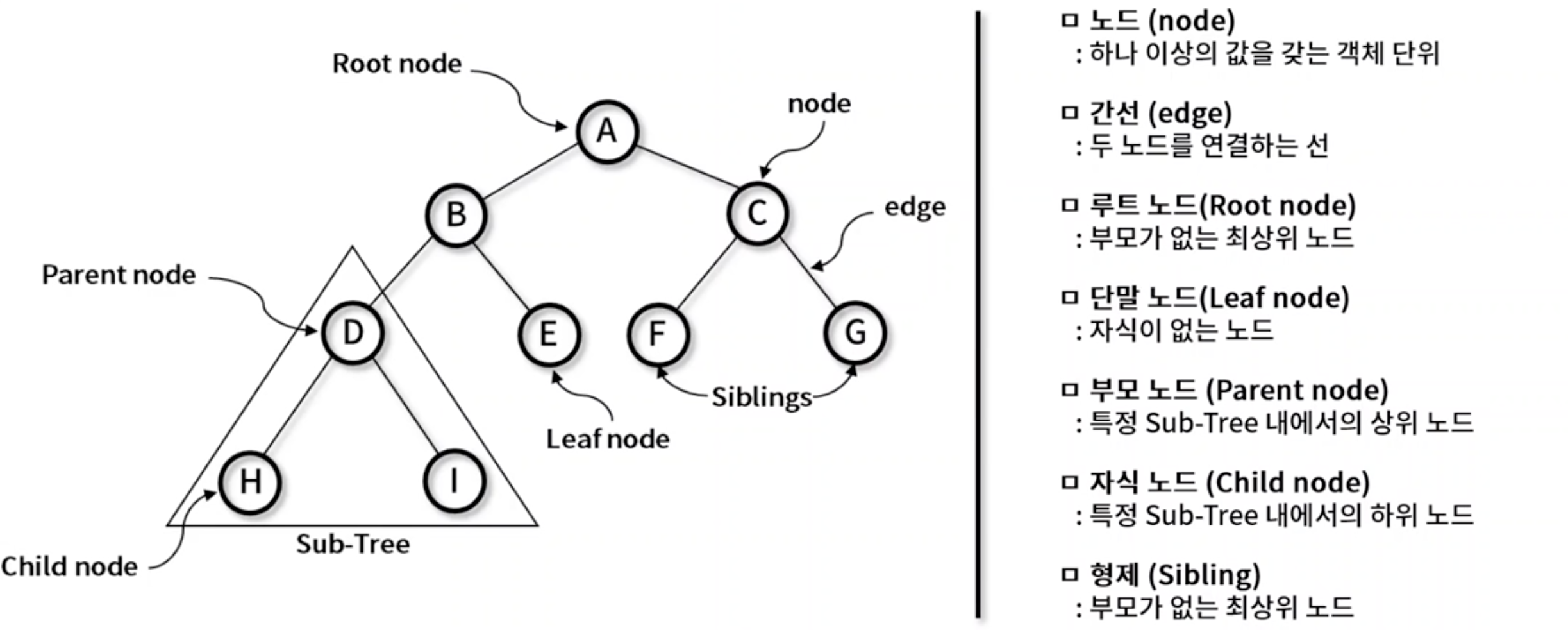
  • 그래프의 일종으로 두 노드 사이의 하나의 간선만 연결되어 있는, 최소 연결과 계층 형태의 비선형 자료 구조
  • 노드 (node) : 하나 이상의 값을 갖는 객체 단위
  • 간선 (edge) : 두 노드를 연결하는 선
  • 루트 노드 (Root node) : 부모가 없는 최상위 노드 (시작 위치)
  • 단말 노드 (Leaf node) : 자식이 없는 노드
  • 부모 노드 (Parent node) : 특정 Sub-Tree 내에서의 상위 노드
  • 자식 노드 (Child node) : 특정 Sub-Tree 내에서의 하위 노드
  • 형제 (Sibling) : 특정 Sub-Tree 내에서 같은 부모를 가리키고 있는 노드
  • 노드 크기 (size) : 자신을 포함한 모든 자손 노드의 개수
  • 노드 깊이 (depth) : 루트에서 특정 노드에 도달하기 위한 간선의 개수 (레벨의 차)
  • 노드 레벨 (level) : 트리의 특정 깊이를 가지는 노드의 집합
  • 노드 차수 (degree) : 노드가 지닌 가지의 수 (바로 하위 자식의 수)
  • 트리 차수 (tree degree) : 트리의 최대 차수
  • 트리 높이 (height) : 루트 노드에서 가장 깊숙이 있는 노드의 깊이


주요 특징

  • 최소 연결 트리
  • 계층 모델
  • 방향 비순환 그래프 (DAG : Directed Acyclic Graph) 중 한 종류


트리 종류

  • 이진 트리
  • 이진 탐색 트리
  • AVL 트리
  • 힙(Heap)



2. 트리 순회

  • 트리 구조에서 각각의 노드를 정확히 한 번씩 체계적인 방법으로 방문하는 과정
  • 필요 용어
  • N (Node) : 해당 노드를 방문
  • L (Left) : 왼쪽 서브 트리로 이동
  • R (Right) : 오른쪽 서브 트리로 이동
  • 순회 방식
  • 전위 순회 (Pre-order) : N - L - R
  • 중위 순회 (In-order) : L - N - R
  • 후위 순회 (Post-order) : L - R - N
  • 층별 순회 (Level-order) : 낮은 Level부터 순차적으로 순회


전위 순회 (Pre-order)

트리

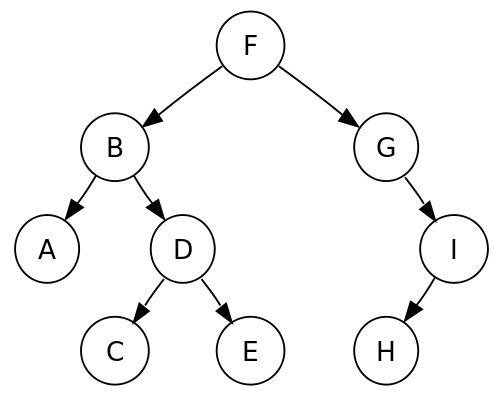
  • 전위 순회 방법 : N - L - R
  • 방문 순서 : F > B > A > D > C > E > G > I < H
    1. 노드를 방문한다.
    2. 왼쪽 서브 트리를 전위 순회한다.
    3. 오른쪽 서브 트리를 전위 순회한다.


의사 코드 (pseudo-code)

preorder(node)
  print node.value
  if node.left !== null then preorder(node.left)
  if node.right !== null then preorder(node.right)



중위 순회 (In-order)

트리

  • 중외 순회 방법 : L - N - R
  • 방문 순서 : A > B > C > D > E > F > G > H > I
  1. 왼쪽 서브 트리를 중위 순회한다.
  2. 현재 노드를 방문한다.
  3. 오른쪽 서브 트리를 중위 순회한다.


의사 코드 (pseudo-code)

inorder(node)
  if node.left !== null then inorder(node.left)
  print node.value
  if node.right !== null then inorder(node.right)



후위 순회 (Post-order)

트리

  • 후위 순회 방법 : L - R - N
  • 방문 순서 : A > C > E > D > B > H > I > G > F
  1. 왼쪽 서브 트리를 후위 순회한다.
  2. 오른쪽 서브 트리를 후위 순회한다.
  3. 노드를 방문한다.


의사 코드 (pseudo-code)

preorder(node)
  if node.left !== null then postorder(node.left)
  if node.right !== null then postorder(node.right)
  print node.value



층별 순회 (Level-order)

트리

  • 층별 순회 방법 : 낮은 Level부터 순차적으로 순회
  • 방문 순서 : F > B > G > A > D > I > C > E > H
    1. root 노드를 방문한다.
    2. Level 증가
    3. 왼쪽에서 오른쪽 순으로 방문


의사 코드 (pseudo-code)

levelorder(root)
  q.enqueue(root)
  while not q.empty do
    node := q.dequeue()
    print node.value
    if node.left !== null q.enqueue(node.left)
    if node.right !== null q.enqueue(node.right)



3. 문제 - 후위 순회

컴퓨터공학과에 들어간 사촌 동생이 후위 순회를 궁금해한다.
트리가 주어졌을 때, 후위 순회하며 방문했던 노드를 산출해주는 프로그램을 작성하시오.
입력은 노드가 추가되는 순번대로 명시된 문자열이 주어지며, 트리를 만들어 갈 때 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 붙여가며 만든다.
왼쪽 - 오른쪽 - 루트 순으로 후위 순회하며 방문한 노드를 배열에 저장하고 그 결화를 반환한다.

function Node(value) {
  this.value = value;
  this.left = null;
  this.right = null;
}

function BinarySearchTree() {
  this.root = null;
}

BinarySearchTree.prototype.insert = function (value) {
  this.root = this._insertNode(this.root, value);
};

BinarySearchTree.prototype._insertNode = function (node, value) {
  if (node === null) {
    node = new Node(value);
  } else if (value < node.value) {
    node.left = this._insertNode(node.left, value);
  } else if (value > node.value) {
    node.right = this._insertNode(node.right, value);
  }

  return node;
};

BinarySearchTree.prototype.postOrderTraverse = function (node, array) {
  if (node === null) {
    return;
  }

  this.postOrderTraverse(node.left, array);
  this.postOrderTraverse(node.right, array);
  array.push(node.value)
};

function answer(str) {
  let result = [];
  // 구현
  let tree = new BinarySearchTree();
  for (let i = 0; i < str.length; i++) {
    tree.insert(str[i]);
  }

  tree.postOrderTraverse(tree.root, result);

  // 구현 종료
  return result;
}

let input = [
  // TC : 1
  "ABC",
  "FBADCEGIH",
  "CBAEDFG",
];

for (let i = 0; i < input.length; i++) {
  process.stdout.write(`#${i + 1}`);
  console.log(answer(input[i]));
}

// #1[ 'C', 'B', 'A' ]
// #2[
//   'A', 'C', 'E',
//   'D', 'B', 'H',
//   'I', 'G', 'F'
// ]
// #3[
//   'A', 'B', 'D',
//   'G', 'F', 'E',
//   'C'
// ]