[수학] 2. 알고리즘 복잡도

in 자료구조 on 수학




1. 알고리즘 평가 지표

  • 정확성
  • 작업량
  • 메모리 사용량
  • 최적성
  • 효율성 (시간 복잡도 + 공간 복잡도)



2. 시간 복잡도

  • 입력 크기의 값에 대해 단위 연산을 몇 번 수행하는지 계산하여, 알고리즘의 수행시간을 평가하는 방법
  • 3가지 점근적 표현법
  • O 빅오 : 최악의 상황을 고려하여 성능 측정 결과 표현 👍
  • Θ 세타 : 평균적인 경우에서의 성능 측정 결과 표현
  • Ω 오메가 : 최선의 상황일 때의 성능 축정 결과 표현


Big-O Complexity Chart

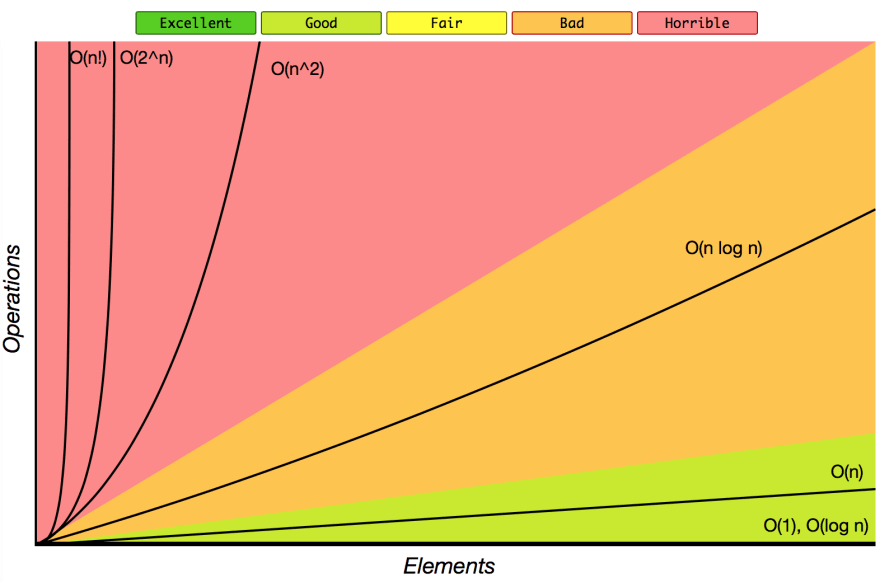
빅오그래프



  • 상수는 O(1)
  • for 문 하나당 n
  • 총 횟수에서 가장 높은 차수 반영한다.



O(1)

function big_o(n) {
    let sum = 0 //1회
    sum = n*2 //1회
    return sum //1회
    // 총 3회 > 상수이므로 O(1)
    // 아주 빠르다
}


O(N)

function big_o(arr, n) {
    let sum = 0 //1회
    for (let i = 0; i< n; i++){
        sum += arr[i]
    } // n회
    return sum //1회
    // 총 n+2회 > O(N)
    // 괜찮은 편
}


O(N2)

function big_o(arr, n) {
    let sum = 0 //1회
    for (let i = 0; i< n; i++){
        for (let j = 0; j<n; j++){
            sum += arr[i]
        }
    } // n * n = n2회
    return sum //1회
    // 총 n2+2회 > O(N2)
    // 많이 느린편
}


O(logN)

function big_o(arr, n) {
    let sum = 0 //1회
    for (let i = 0; i< n; i *=2){
        sum += 2
    }
    // 절반 수행
    // 나누는 수에 log 붙여주면 된다
    // n 보다 빠르다 
    // n / 2 회
    return sum //1회
    // 총 n/2 + 2 = O(logN)
}



나의 회고 🤫

코테 준비하면서 시간 복잡도 생각하기!!
코드가 짧은게 좋느냐, 시간이 짧은게 좋느냐 가 항상 딜레마인데, 한쪽이 너무 우세하다면 그 쪽으로 코딩하기!